M203 20251206 Lecture 13 Quadratics and Conics
Session 3: Quadratics
1. Factoring Quadratics
1 ) How many integers $x$ satisfy the equation $(x^2 – x - 1)^{x+2} =1$
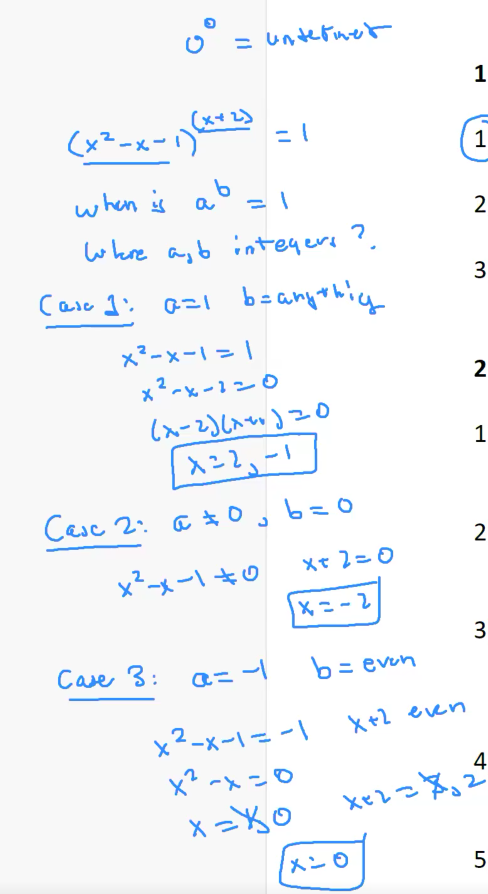
2 ) Find all possible values of $a/b$ if $a^2+ 4b^2 = 4ab$
Homogeneous Equation: every term has the same degree

问题: Find the possible values of $a/b$ if $a^3-3ab^2+2b^3=0$


2. Relating Roots and Coefficients
1 ) Let r and s be the roots of $x^2 – px + q = 0$. In this problem, we find $r^2 + s^2$ in term of $p$ and $q$.
$r^2+s^2=(r+s)^2-2rs=p^2-2q$

问题: Find $r^3 + s^3$ in terms of $p, q$.
$r^3 + s^3 = (r+s)(r^2 - rs + s^2) = p(p^2 - 2q - q) = p^3 - 3pq$
$(r+s)(r^n + s^n) = r^{n+1} + rs^n + sr^n + s^{n+1}$
$= r^{n+1} + s^{n+1} + rs(r^{n-1} + s^{n-1})$
$r^{n+1} + s^{n+1} = (r+s)(r^n + s^n) - rs(r^{n-1} + s^{n-1})$
$$r^{n+1} + s^{n+1} = (r+s)(r^n + s^n) - rs(r^{n-1} + s^{n-1})$$
说明: 高阶的公式可以通过低阶的公式进行递推求解。例如:
- 已知 $r + s$ 和 $r^2 + s^2$,可以求出 $r^3 + s^3$
- 已知 $r^2 + s^2$ 和 $r^3 + s^3$,可以求出 $r^4 + s^4$
3. The discriminant

19 . If the graph of the equation $y=ax^2+6$ is tangent to the graph of $y=x$. What is $a$?
4 ) Let $f(x) = (5x^2 – 4x + 8) / (x^2 + 1)$, where the domain of $f$ is all real numbers. Find the range of $f(x)$.

5 ) Let $f(x) = (7x^2 – 4x + 4)/(x^2 + 1)$ where the domain of $f$ is all real numbers. Find the range of $f$.
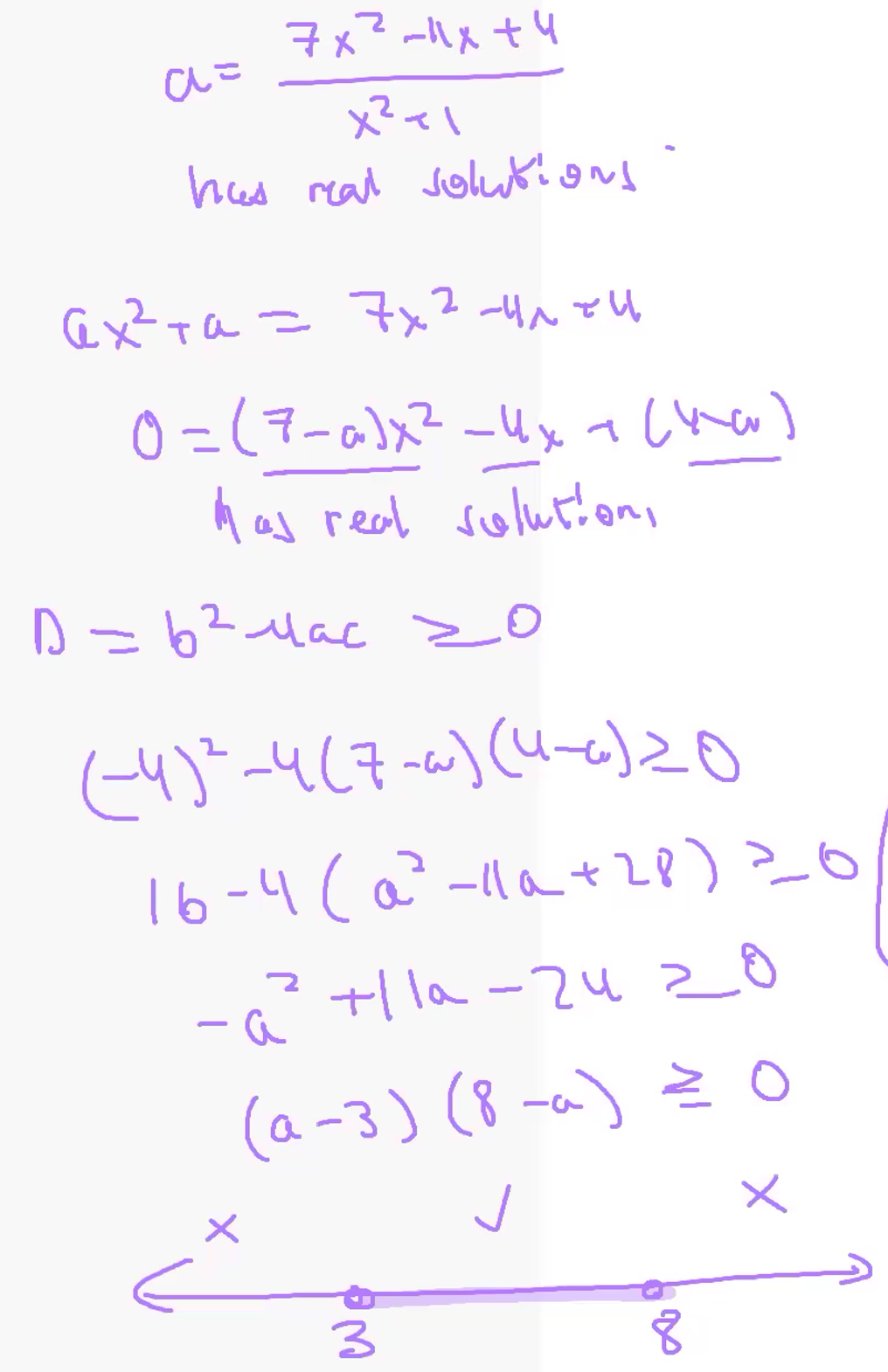
Session 4: Conics
What is Conics
Two forms:
$y=a(x-h)^2 + k$ Vertex $(h,k)$ and Symmetry line is $x=k$.
$x=a(y-k)^2 + h$ Vertex $(h,k)$ and Symmetry line is $y=h$.

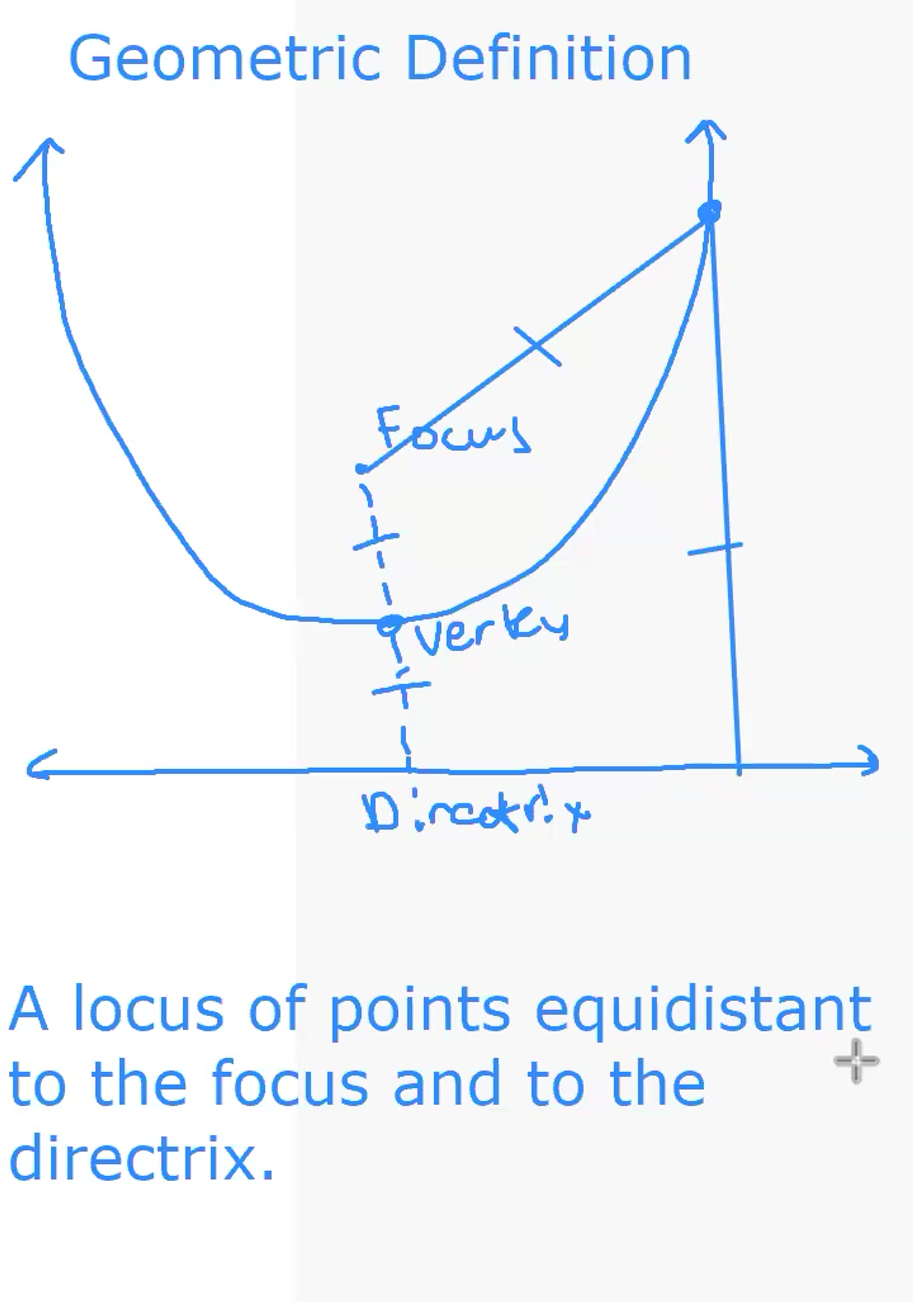
A parabola is the locus of points in a plane that are equidistant from a given line and a point not one the line. The line is called the directrix of the parabola and the point is the parabola’s focus.
- Property 1: Any point on the parabola is equidistant from the directrix and from focus.
- Property 2: The vertex of a parabola is the midpoint of the segment that connects the focus of the parabola to the point where the parabola’s axis
of symmetry intersects the parabola’s directrix.
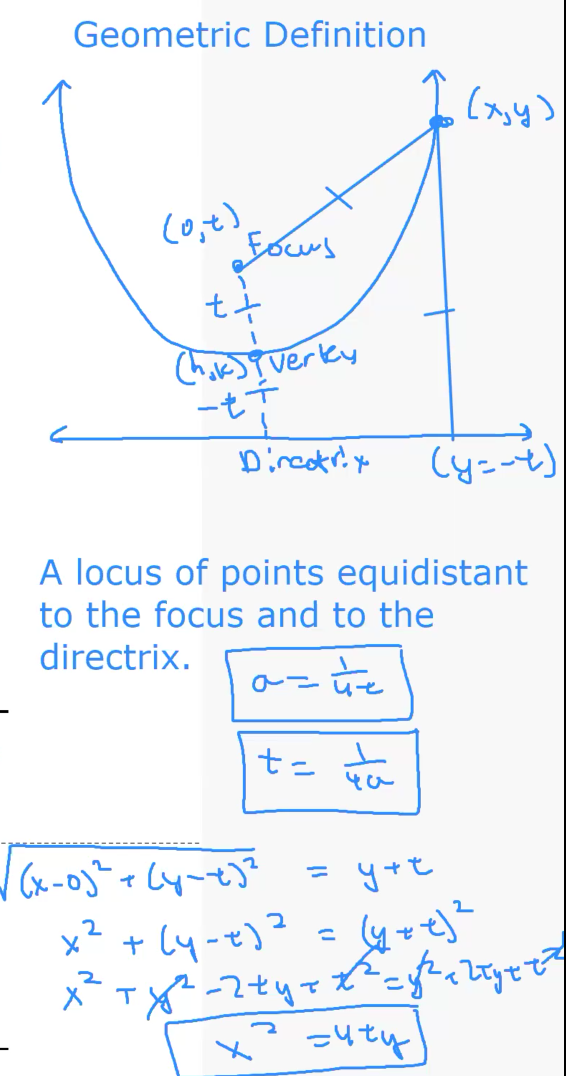
1 . Suppose a parabola has focus $(0,t)$ and vertex $(0,0)$, where $t>0$. The parabola is written in the form of $y=ax^2$. Find the equation of the directrix of the parabola. What is the relationship of $a$ and $t$?

2 ) Find the equation whose graph is a parabola with vertex $(0,0)$ and focus $(0,2)$.

3 ) Find the equation whose graph is a parabola with vertex $(-6,3)$ and focus $(-6,5)$.
9) What is the directrix of a parabola with focus (3,7) and vertex (2,5)?
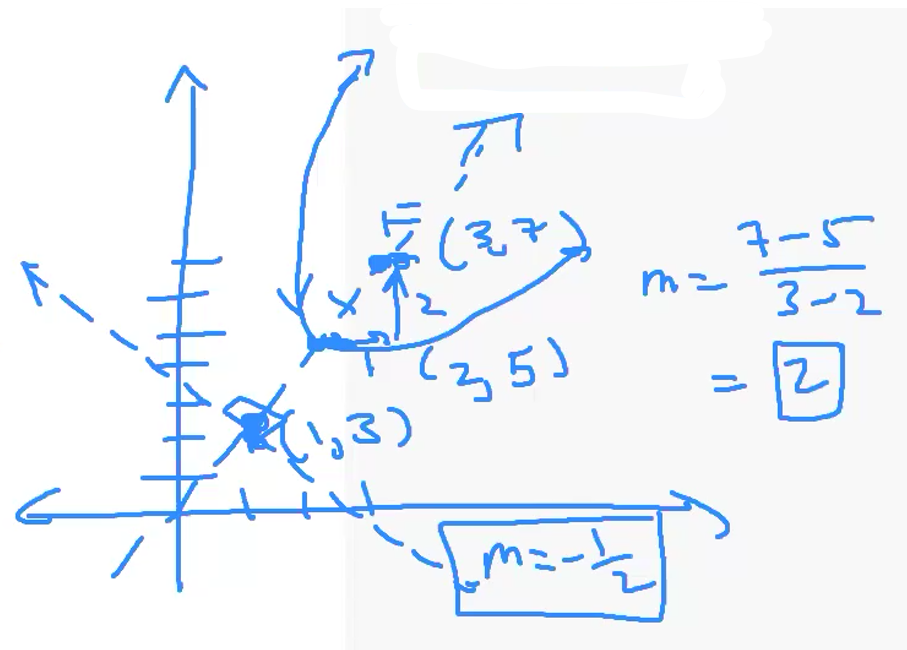
$y-3=-\dfrac{1}{2}(x-1)$
7 ) Find the vertex and axis of symmetry of the graph of $y^2-8y+x=2$.
14 ) A parabolic arch has a height of 20 feet and a span of 30 feet. How high is the arch 6 feet from its center?
16 )Find the equation whose graph is a horizontally-opening parabola that passes through $(20,-3)$ $(12,1)$ and $(33,2)$
Tick: plug into unsimplified equation $x=ay^2+by+c$
17 ) A parabolic arch is 30 meters wide at its base. A fly sits on the arch 25 meters above a point on the ground that is 5 meters from one point where the arch touches the ground. How high is the center of the arch?
Method 1:

Method 2:
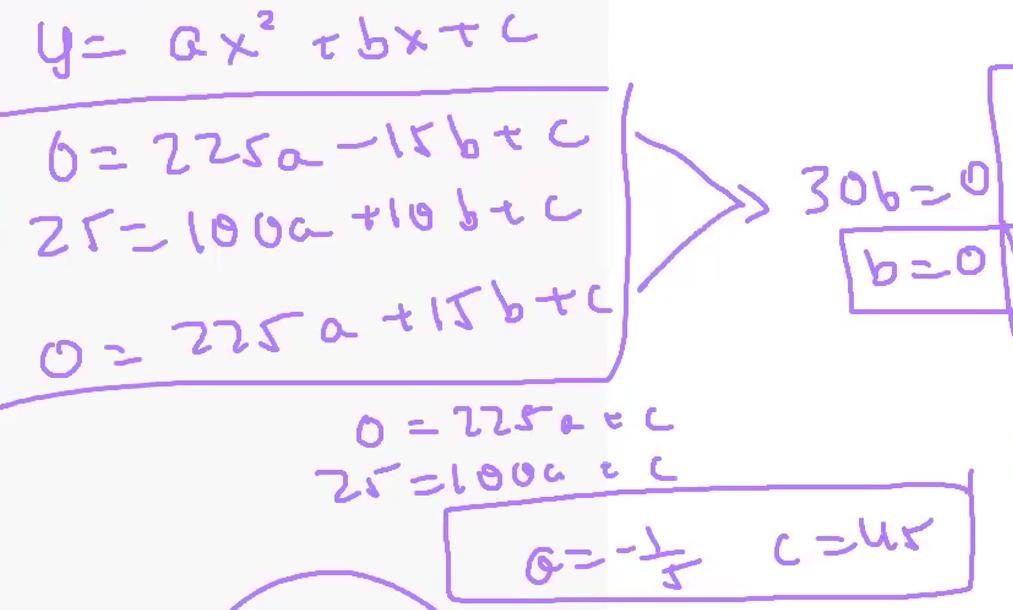
18 ) The graph of $y=x^2+2x-2$ is reflected over the line $y=x$. How many points of intersections does the original graph have with its reflection?

